在样本量计算的过程，我们经常会遇到非劣效设计或者是优效性设计的情况，本文就从样本量估算的公式入手，跟大家一起看一下非劣效和优效性经验的样本量估算，以及随着界值的变化样本量的变化情况。

假设一个简单的情况，即两组样本例数和标准差一致，此时其中一组的样本量计算公式为：

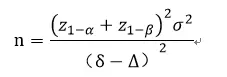
上式中σ为两组标准差，δ为两组的均数差值，Δ为界值。回忆一下两组均数比较的样本量计算公式：

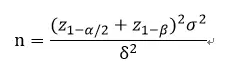
比较一下我们就会发现两个公式很像，只是分母处多了一个Δ，而Δ恰恰又是我们需要设定的两组可接受的差异大小。

再看非劣效/优效的公式，如果取α=0.025，β=0.1，此时(Z1-α+Z1-β)的平方为10.5左右，n=10.5×（σ/（δ-Δ））2。

σ为两组的标准差，一定为正数，此时的样本量n就由（δ-Δ）来决定了，分子（δ-Δ）越小，样本量越大。下面看一下两种情况：

1、非劣效情况下

非劣效的检验假设：H0为试验组-对照组≤-Δ，H1为试验组-对照组＞-Δ

δ为两组的均数差值，是试验组减去对照组，此时一般为负数。

Δ为界值，如果是非劣效检验Δ为负数，此时Δ绝对值越大，δ-Δ的绝对值越大，所以δ-Δ的平方越大。所需要的样本量越小。

2、优效情况下

非劣效的检验假设：H0为试验组-对照组≤Δ，H1为试验组-对照组＞Δ

δ为两组的均数差值，是试验组减去对照组，此时一般为正数。

Δ为界值，如果是优效检验Δ为正数，此时Δ越大，δ-Δ越小，所以δ-Δ的平方越小。所需要的样本量越大。