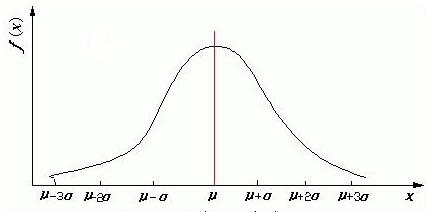
在概率统计的学习或使用过程中，经常有人会提到大数定律和中心极限定理，它们也恰恰是概率论、统计学和理论科学的基石。但是肯定有人在突然听到它们的名字时，还会很讶异，心里嘀咕这到底是什么意思。为了让大家对这两个概念时有所了解，今天我们就一起来聊一下这两个问题。

上面就是大数定律（Law Of Large Numbers）的数学表达形式，它描述了在随机事件大量重复出现时，结果往往呈现几乎必然的规律。说人话就是，在试验不变的条件下，随机事件出现的频率近似于它的概率，也就是样本量很大的时候，样本统计量与总体参数充分接近。

对于大数定律，举个例子就更明白了。重复投掷一枚硬币，多次重复后出现正面的频率逐渐正面的概率（1/2）；又如称量某物体的重量，假如秤没有问题（即不存在系统误差），对同一物体多次称量求均数代表物体的重量，如果称量次数越多，结果越接近物体的真实重量。

大数定律有不同的数学家对其进行证明并以数据家的名字命名，常见的有：伯努利大数定律、辛钦大数定律、柯尔莫哥洛夫强大数定律和重对数定律。有了大数定律，我们就可以确信，为求一个随机变量的期望，我们只需要把它测量多次，然后取均数便可。但是需要注意的是，这个定律并没有告诉我们需要测量多少次才算可以。

大数定律揭示了大量随机变量的平均结果，但是没有涉及到随机变量的分布问题，而中心极限定理说明在一定条件下，大量独立随机变量的均数以正态分布为极限。下面再来看看中心极限定理（Central Limit Theorem）的简单数学表达： 

上面就是中心极限定理的数学表达，其中独立同分布是指随机序列/变量有相同的概率分布，并且之间相互独立。同样中心极限定理也不止一个，它们是阐述大量的相互独立的随机变量的线性组合在一定条件下近似服从正态分布的一系列定理。

简单地说，中心极限定理是指在大样本条件下，不论总体的分布如何，样本均值的分布总是近似地服从正态分布，且样本均数的均数等于原总体的均数，样本均数的标准差等于原标准差/根号n。

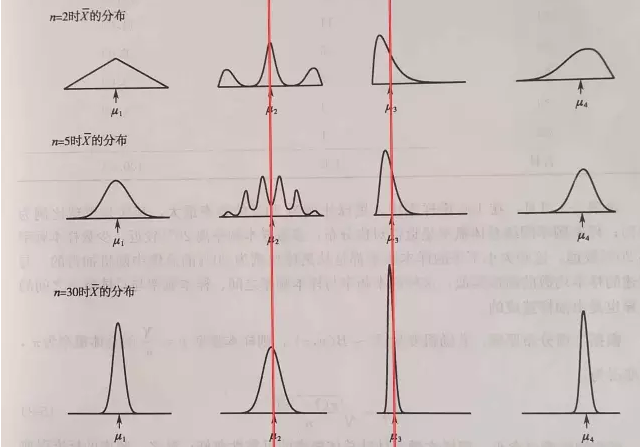
那么什么才叫大样本呢？有模拟显示每次抽样30例及以上，样本均数的分布就近似于正态分布。如下图（第1行为总体分布，第2行为n=2的均数分布，第3行为n=5的均数分布，第4行为n=30的均数分布）：