线性回归是统计里比较基础的内容之一，不知道小伙伴们都做过没有，没有做过的也没有关系，我们今天先讲一下怎么做；至于做过的小伙伴，也可以快速看一下注意事项，再想想曾经做的那些统计做对了吗？

线性回归就是探讨一个或多个自变量与因变量的定量关系，简单地说就是探讨自变量增加一个或几个单位，因变量增加（或减少）几个单位，包括直线回归和非直接回归。下面以直线回归中的简单回归（一个自变量）为例，看SPSS怎么操作。

一个研究想看身高（height）对肺活量（vcp）的影响，收集了29个人的数据，怎么做线性回归呢？

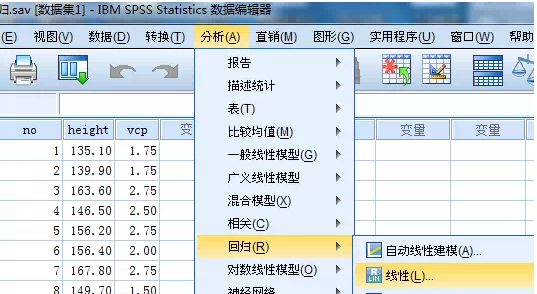
在SPSS菜单点击“分析”－“回归”－“线性”，在弹出的对话里将肺活量选入因变量，身高选入自变量，点击确定。

在回归结果，我们看到三个表格，如下图：

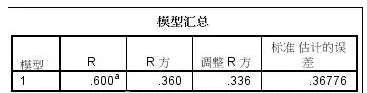
在第一个“模型汇总”表里，我们看到R、R方及调整R方，在简单线性回归模型时，这里的R相当于自变量与因变量的pearson相关系数；R方即前面R的平方，意义是有多大比例的因变量变异能被自变量解释，在这里即肺活量的36%的变量可以由身高解释（影响）；调整R方在简单线性回归没有太多意义，在多重线性回归模型里，可以通过查看增加或减少某个自变量后调整R方的变化来决定是否在模型里保留某变量。

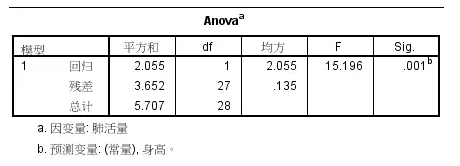
上表是判断方程模型是否成立的方差检验，在这里，它的P值与自变量系数检验的P值相等，在多重线性回归里，只要有一个自变量对因变量的影响有统计学意义，此检验的P值都会小于0.05，也即如果此检验P值不小于0.05，可认为所有自变量与因变量都没有线性关系。

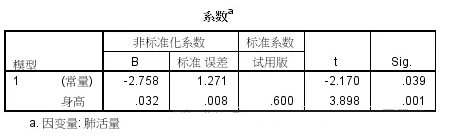
上表是我们会写进文章里的结果，非标准化β值即方程的系数，上表的方程模型可以写成vcp＝0.032*height-2.758+ε，ε为随机误差项，即身高增加1cm，肺活量增加0.032；第三个数0.6是标准化系数，主要用于多个自变量时比较哪个自变量对因变量影响更大；第二个数0.008是非标准系数的标准误，根据其与非标准化系数可以计算t，根据t及自由度可以查表得出P值。

到此小伙伴们是不是认为回归做完了呢？答案是否定的，线性回归模型还要满足以下5个条件：独立、正态、线性、等方差和无异常值或强影响点。

独立：即我们数据是各个case是独立的，不能有一个人测量两次或者多次数据，或者对称器官的数据作为两条数据使用，主要从数据来源判断数据是否独立。

正态：回归分析对自变量及因变量的分布均没有要求，因此正态不是指因变量或自变量正态，而是指回归之后的残差正态，具体检验方法：在回归对话框里点击“保存”按钮，如下图选择未标准差残差：

这样在数据集最后一列多出一列变量，即未标准化残差，可检查此残差是否符合正态分布。

线性：是看自变量与因素是否有线性关系。主要查看两个变量的散点图，观察是否线性关系。

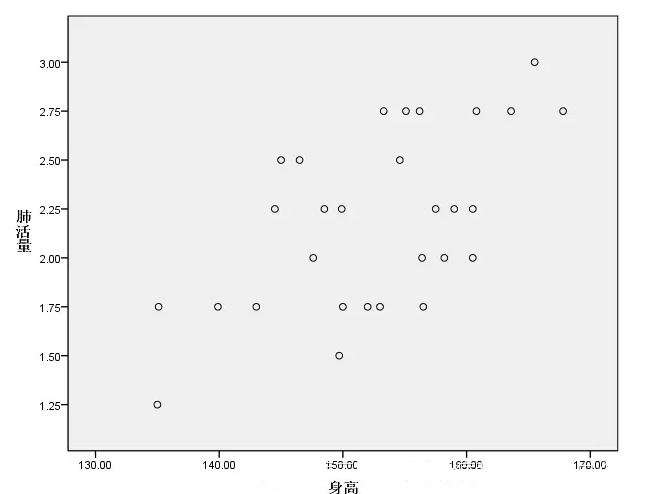
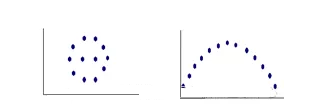
如下图可以认为两者有线性关系。如果如下图数据如果直接做回归分析，可能都没有线性关系（r=0），但观察散点图，左侧认为没有线性关系，右侧有曲线关系（抛物线）。因此散点图在相关及回归分析中至关重要。

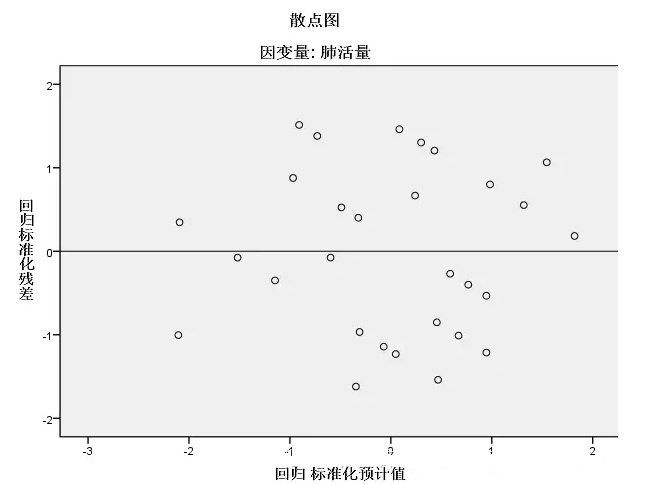
等方差：等方差不是指因变量或自变量方差相等，而是在因变量的每个预测值处，残差的方差相等。在SPSS里可以直接画残差与因变量预测值的散点图查看，如下图所示：

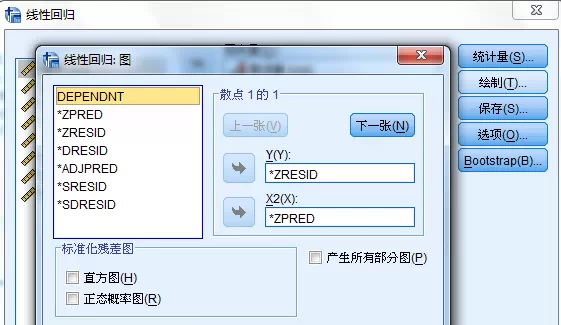
结果如下图，如果随着预测值变量，残差在预测值上下分布分布基本相同，可以认为残差相等。

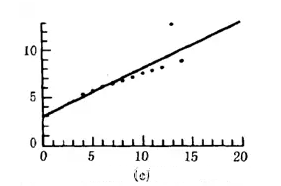
异常值或强影响点：即某一个或几个点可能会对线性关系影响很大，这一组（或几组）数往往是离群值，因此可以通过画因变量与自变量的散点图查看。本例子中散点图见前面的图，认为没有观察到强影响点。如下图可认为有强影响点，是否为异常值需要再查看数据或进行专业判断。

在多重线性回归中，除要满足上述要求外，还要满足各自变量间没有共线性，我们下次再进行专门探讨。

看完了今天的内容，小伙伴们是不是想问，如果以上条件如果其中一个或多个不满足怎么办呢？统计学家已经想到并解决了这个问题，不过再细讲就复杂了，建议查看相关书籍或询问相关统计学专家。