数学是一门确定的科学，它的美在于任何一位理智的人都会对某一数学陈述给出明确的答案，比如：±2是方程x2-4=0的两个实数解，又如2+3=5。没有任何一门学科能够享受这种奢华的肯定性，尽管宗教号称自己是绝对真理，但仍旧不被所有人相信。

在现实生活中，偶然事件扮演着重要的角色，当数学遇到了偶然，便催生了概率论。下面我们来看一个概率论的问题。

问题：假设有n个人参加聚会，其中至少有两个人生日相同的概率是多少呢（P（A））？（条件是一年有365天，每个人的生日随机发生在一年中的某一天。）

简单的解法是我们把n个人所有可能的生日组合都列出来（它等于365的n次方），然后找出其中至少有两个人生日相同的个数，再除以总个数就可以得出概率P（A）。显然这样算是十分困难的。

那我们不妨换一个思路，我们求这n个人中大家生日都不相同的个数，它等于365×364×363×……×（365-n+1）。为什么是这样呢？因为第1个人的生日有365个选择，第2人为了和第1个人生日不一样就只有364个选择了，依此类推。

获得了上面的结果，我们就可以算出：

用现实来理解一下那个公式，假如有366个人，那么必定有两个人的生日相同，概率为1；如果只有2个人，公式得出概率为1/365，当然是正确的。

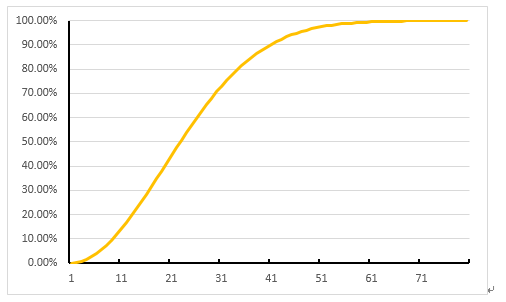
这样题就解完了，但是有一个有趣的事情是：当n≥23时，至少有两个人生日相同的概率就大于50%，当房间里有70个人时，那么至少有两个人生日相同的机会就会大到99.9%。

回想一下，在你大学的班级里又有多少人错过了一段“同日生”的缘分呢。

为什么会是上面的结果呢？我们不妨来把n和P（A）做个图看看。