某位研究者做一个RCT研究，研究对象入组时测量A指标，然后随机分为试验组和对照组，试验组进行干预，对照组不进行处理，过6个月再次测量A指标，得到以下几个结果。

研究者比较了T0和C0，差异没有统计学意义；又比较了C0和C6，差异也没有统计学意义；因此研究者得到T0、C0、C6认为是相等的。研究者比较了T0和T6，差异有统计学意义，因此推论C6和T6差异有统计学意义。但对结果不太确定，过来咨询，小伙伴们觉得能进行这种推论吗？

显然这种推论是不成立的。统计学比较的结果不具有传递性，举个简单的例子，把上述例子换成具体数字，如下表。我们假设所有标准差相同，当均值相差5个单位以上时，差异有统计学意义。我们发现T0和C0差1个单位，差异没有统计学意义；C0、C6差四个单位，差异无统计学意义；但T0和C6差异5个单位，差异有统计学意义，也即T0、C0、C6逐渐增加，从量变积累为质变。同理，T0和T6差异8个单位，差异有统计学意义，但不能推出T6和C6差异有统计学意义。

对于RCT试验，我们一般的分析方法是先比较T0和C0，检查基线是否均衡，然后再比较T6和C6；再者也可以先计算6个月与基线的差值，然后比较两组差值的差异，当然也可以尝试进行协方差分析。我于是追问为什么不进行常规的方法分析？大家肯定也猜到了结果，就是6个月时两组的比较差异没有统计意义，阳性结果是每个研究者的追求，他也不例外。

说到这里，想给大家讲一个故事，其背后的问题大家自己品味。某国进行大选，有A、B、C三名候选人，分别在三个州进行普选调查，结果如下：

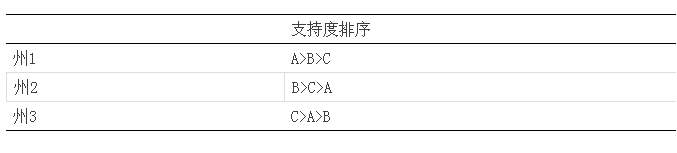
即在第一个州，对A候选人的支持度最高，其它是B候选人，对C支持度最低，其它类似。于是A候选人开始宣传“相对于B候选人，2/3的人更愿意选我”； B候选人开始宣传“相对于C候选人，2/3的人更愿意选我”；C候选人开始宣传“相对于A候选人，2/3的人更愿意选我”。从表中来看，三位候选人的宣传看似矛盾，但都没有错误，他们都是聪明的候选人。